动态规划(英语:Dynamic programming,简称 DP)是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划常常适用于有重叠子问题和最优子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。
动态规划背后的基本思想非常简单。大致上,若要解一个给定问题,我们需要解其不同部分(即子问题),再根据子问题的解以得出原问题的解。动态规划往往用于优化递归问题,例如斐波那契数列,如果运用递归的方式来求解会重复计算很多相同的子问题,利用动态规划的思想可以减少计算量。
通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,具有天然剪枝的功能,从而减少计算量:一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。
🔗 给定一个三角形,找出自顶向下 的最小路径和。每一步只能移动到下一行中相邻的结点上。
相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。
例如,给定三角形:
1 2 3 4 5 6 [ [2], [3,4], [6,5,7], [4,1,8,3] ]
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
**说明:**如果你可以只使用 O (n ) 的额外空间(n 为三角形的总行数)来解决这个问题,那么你的算法会很加分。
设状态 f ( i , j ) {f(i,j)} f ( i , j ) ( i , j ) {(i,j)} ( i , j ) 状态转移方程 为:
f ( i , j ) = m i n { f ( i + 1 , j ) , f ( i + 1 , j + 1 ) } + ( i , j ) {f(i,j) = min\{f(i+1,j), f(i+1,j+1)\} + (i,j)} f ( i , j ) = m i n { f ( i + 1 , j ) , f ( i + 1 , j + 1 ) } + ( i , j )
1 2 3 4 5 6 7 8 9 10 11 public int minimumTotal (List<List<Integer>> triangle) for (int i = triangle.size() - 2 ; i >= 0 ; --i){ for (int j = 0 ; j < i + 1 ; ++j){ int curnum = triangle.get(i).get(j); triangle.get(i).set(j, curnum + Math.min( triangle.get(i+1 ).get(j), triangle.get(i+1 ).get(j+1 ))); } } return triangle.get(0 ).get(0 ); }
🔗 给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2, 1, -3, 4, -1, 2, 1, -5, 4]
**进阶:**如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的分治法求解。
从头到尾遍历这个数组,对于数组里的一个整数,分为两种情况:
如果之前的subArray的总体和大于0的话,认为其对后续结果是有贡献的,此时允许加入之前的subArray;
如果之前的subArray的总体和小于等于0的话,认为其对后续结果是没有贡献的,此时另起一个subArray;
设状态为 f [ j ] {f[j]} f [ j ] S [ j ] {S[j]} S [ j ] 状态转移方程 如下:
f [ j ] = m a x { f [ j − 1 ] + S [ j ] , S [ j ] } {f[j]=max\{f[j-1]+S[j],S[j]\}} f [ j ] = m a x { f [ j − 1 ] + S [ j ] , S [ j ] } 1 ≤ j ≤ n {1 \leq j \leq n} 1 ≤ j ≤ n
t a r g e t = m a x { f [ j ] } {target = max\{f[j]\}} t a r g e t = m a x { f [ j ] } 1 ≤ j ≤ n {1 \leq j \leq n} 1 ≤ j ≤ n
1 2 3 4 5 6 7 8 9 10 11 12 public int maxSubArray (int [] nums) int max = nums[0 ]; for (int i = 1 ; i < nums.length; ++i){ if (nums[i] < nums[i-1 ] + nums[i]){ nums[i] += nums[i-1 ]; } if (nums[i] > max){ max = nums[i]; } } return max; }
🔗 给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回符合要求的最少分割次数 。
示例:
输入: “aab”
定义状态 f ( i , j ) {f(i,j)} f ( i , j ) [ i , j ] {[i,j]} [ i , j ]
f ( i , j ) = m i n { f ( i , k ) + f ( k + 1 , j ) } , i ≤ k ≤ j , 0 ≤ i ≤ j < n {f(i,j)=min\{f(i,k)+f(k+1,j)\}, i \leq k \leq j, 0 \leq i \leq j < n} f ( i , j ) = m i n { f ( i , k ) + f ( k + 1 , j ) } , i ≤ k ≤ j , 0 ≤ i ≤ j < n
这是一个二维函数,实际写代码比较麻烦。所以要转换成一维DP。
如果每次,从i往右扫描,每找到一个回文就算一次DP的话,就可以转换成 f ( i ) = {f(i)=} f ( i ) = [ i , n − 1 ] {[i,n-1]} [ i , n − 1 ]
f ( i ) = m i n { f ( j + 1 ) + 1 } , i ≤ j < n {f(i)=min\{f(j+1)+1\},i \leq j < n} f ( i ) = m i n { f ( j + 1 ) + 1 } , i ≤ j < n
一个问题出现了,就是如何判断 [ i , j ] {[i,j]} [ i , j ] P [ i ] [ j ] = t r u e P[i][j]= true P [ i ] [ j ] = t r u e [ i , j ] [i,j] [ i , j ]
P [ i ] [ j ] = s t r [ i ] = = s t r [ j ] & & P [ i + 1 ] [ j − 1 ] P[i][j]=str[i]==str[j] \&\& P[i+1][j-1] P [ i ] [ j ] = s t r [ i ] = = s t r [ j ] & & P [ i + 1 ] [ j − 1 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public int minCut (String s) int [] dp = new int [s.length()+1 ]; boolean [][] p = new boolean [s.length()][s.length()]; for (int i = 0 ; i <= s.length(); ++i){ dp[i] = s.length() - i - 1 ; } for (int i = s.length() - 1 ; i >= 0 ; --i){ for (int j = i; j < s.length(); ++j){ if (s.charAt(i) == s.charAt(j) && (j - i < 2 || p[i+1 ][j-1 ])){ p[i][j] = true ; dp[i] = Math.min(dp[i], dp[j+1 ] + 1 ); } } } return dp[0 ]; }
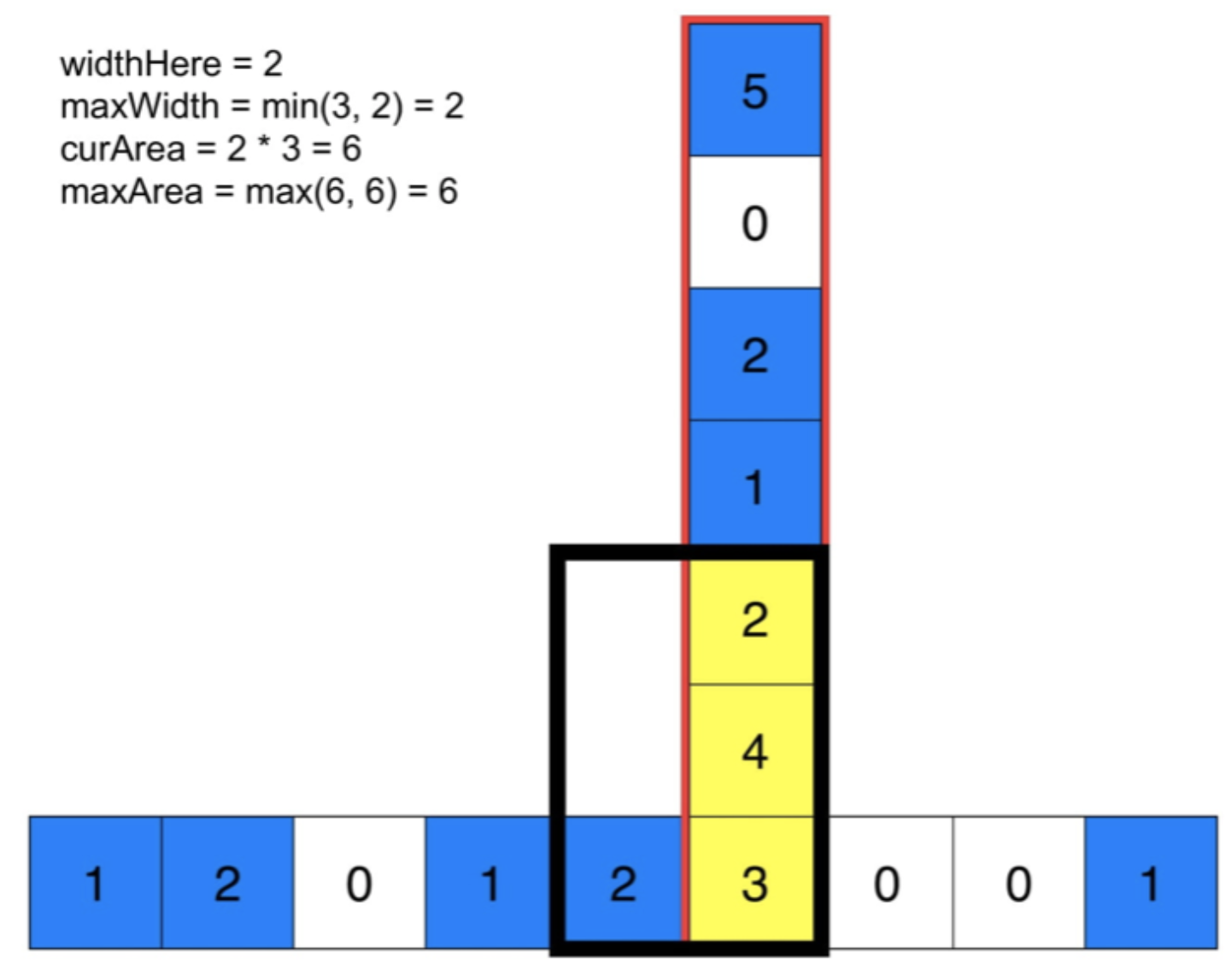
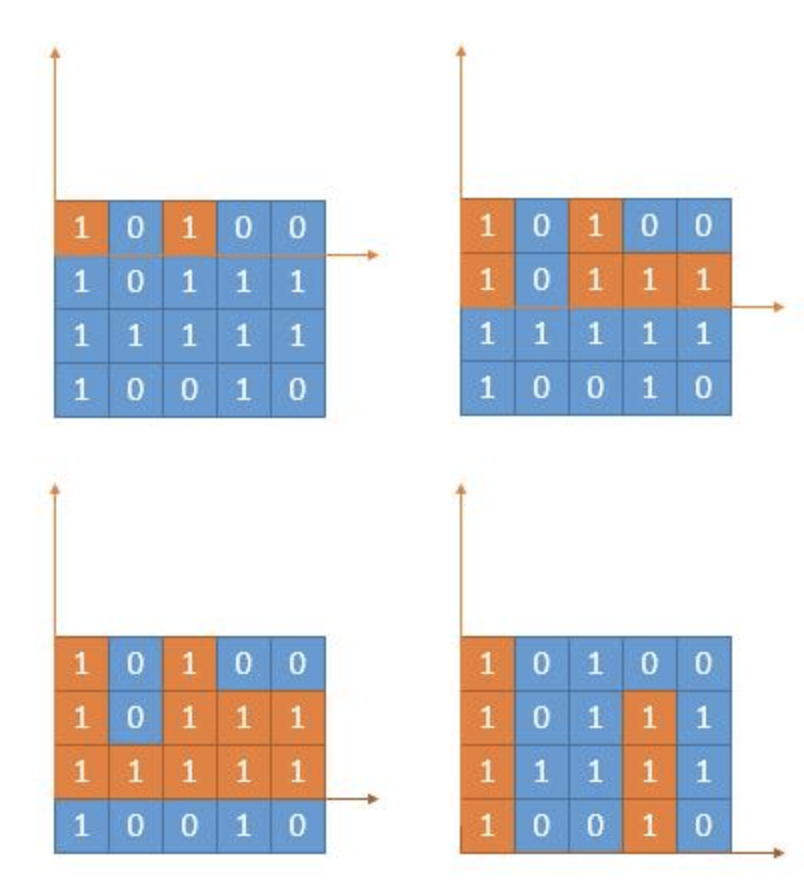
🔗 给定一个仅包含 0 和 1 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例:
1 2 3 4 5 6 7 8 输入: [ ["1" ,"0" ,"1" ,"0" ,"0" ], ["1" ,"0" ,"1" ,"1" ,"1" ], ["1" ,"1" ,"1" ,"1" ,"1" ], ["1" ,"0" ,"0" ,"1" ,"0" ] ] 输出: 6
先对每一行进行处理如下,以常数时间计算出在给定的坐标结束的矩形的最大宽度;
一旦我们知道了每个点对应的最大宽度,我们就可以在线性时间内计算出以该点为右下角的最大矩形。当我们遍历列时,可知从初始点到当前点矩形的最大宽度,就是我们遇到的每个最大宽度的最小值。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution public int maximalRectangle1 (char [][] matrix) if (matrix.length == 0 ){ return 0 ; } int maxarea = 0 ; int [][] dp = new int [matrix.length][matrix[0 ].length]; for (int i = 0 ; i < matrix.length; i++){ for (int j = 0 ; j < matrix[0 ].length; j++){ if (matrix[i][j] == '1' ){ dp[i][j] = j == 0 ? 1 : dp[i][j-1 ] + 1 ; int width = dp[i][j]; for (int k = i; k >= 0 ; k--){ width = Math.min(width, dp[k][j]); maxarea = Math.max(maxarea, width * (i - k + 1 )); } } } } return maxarea; } }
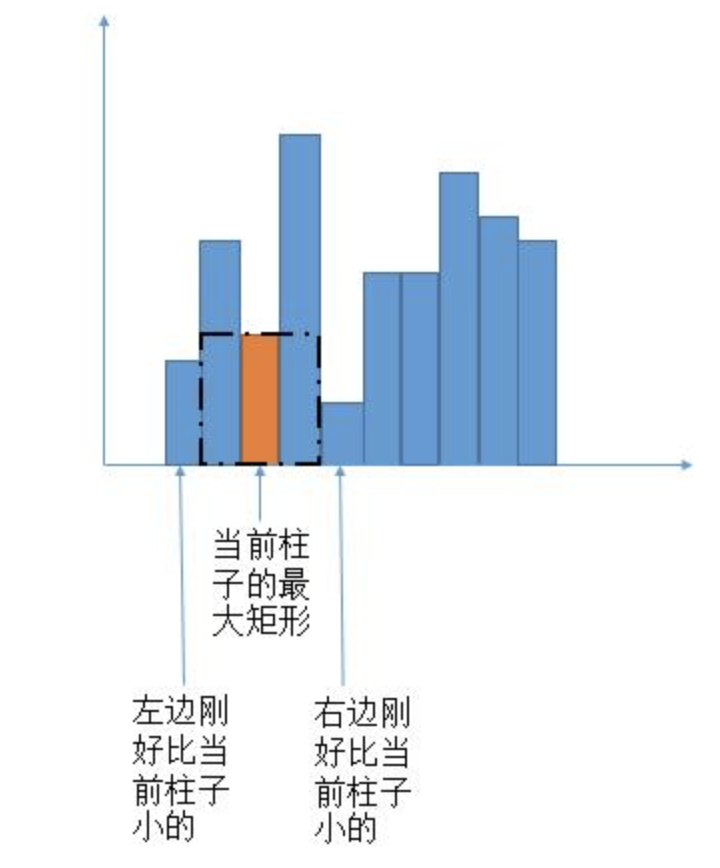
🔗 的栈解法看下边的橙色的部分,这完全就是LeetCode-84呀!
根据LeetCode-84的两种不同解法(栈和求边界),得出本题如下两种方法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 public int maximalRectangle (char [][] matrix) if (matrix.length == 0 ) { return 0 ; } int [] heights = new int [matrix[0 ].length]; int maxArea = 0 ; for (int row = 0 ; row < matrix.length; row++) { for (int col = 0 ; col < matrix[0 ].length; col++) { if (matrix[row][col] == '1' ) { heights[col] += 1 ; } else { heights[col] = 0 ; } } maxArea = Math.max(maxArea, largestRectangleArea(heights)); } return maxArea; } public int largestRectangleArea1 (int [] heights) Stack<Integer> stack = new Stack<>(); stack.push(-1 ); int maxarea = 0 ; for (int i = 0 ; i < heights.length; ++i) { while (stack.peek() != -1 && heights[stack.peek()] >= heights[i]) maxarea = Math.max(maxarea, heights[stack.pop()] * (i - stack.peek() - 1 )); stack.push(i); } while (stack.peek() != -1 ) maxarea = Math.max(maxarea, heights[stack.pop()] * (heights.length - stack.peek() - 1 )); return maxarea; } public int largestRectangleArea2 (int [] heights) if (heights.length == 0 ) { return 0 ; } int [] leftLessMin = new int [heights.length]; leftLessMin[0 ] = -1 ; for (int i = 1 ; i < heights.length; i++) { int l = i - 1 ; while (l >= 0 && heights[l] >= heights[i]) { l = leftLessMin[l]; } leftLessMin[i] = l; } int [] rightLessMin = new int [heights.length]; rightLessMin[heights.length - 1 ] = heights.length; for (int i = heights.length - 2 ; i >= 0 ; i--) { int r = i + 1 ; while (r <= heights.length - 1 && heights[r] >= heights[i]) { r = rightLessMin[r]; } rightLessMin[i] = r; } int maxArea = 0 ; for (int i = 0 ; i < heights.length; i++) { int area = (rightLessMin[i] - leftLessMin[i] - 1 ) * heights[i]; maxArea = Math.max(area, maxArea); } return maxArea; }
方法二中套用的栈的解法,我们其实可以不用调用函数,而是把栈糅合到原来求 heights 中。因为栈的话并不是一次性需要所有的高度,所以可以求出一个高度,然后就操作栈。
里边有一个小技巧,84 题 的栈解法中,我们用了两个 while 循环,第二个 while 循环用来解决遍历完元素栈不空的情况。其实,我们注意到两个 while 循环的逻辑完全一样的。所以我们可以通过一些操作,使得遍历结束后,依旧进第一个 while 循环,从而剩下了第 2 个 while 循环,代码看起来会更简洁。
那就是 heights 多申请一个元素,赋值为 0。这样最后一次遍历的时候,栈顶肯定会大于当前元素,所以就进入了第一个 while 循环。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 public int maximalRectangle (char [][] matrix) if (matrix.length == 0 ) { return 0 ; } int [] heights = new int [matrix[0 ].length + 1 ]; int maxArea = 0 ; for (int row = 0 ; row < matrix.length; row++) { Stack<Integer> stack = new Stack<Integer>(); heights[matrix[0 ].length] = 0 ; for (int col = 0 ; col <= matrix[0 ].length; col++) { if (col < matrix[0 ].length) { if (matrix[row][col] == '1' ) { heights[col] += 1 ; } else { heights[col] = 0 ; } } if (stack.isEmpty() || heights[col] >= heights[stack.peek()]) { stack.push(col); } else { while (!stack.isEmpty() && heights[col] < heights[stack.peek()]) { int height = heights[stack.pop()]; int leftLessMin = stack.isEmpty() ? -1 : stack.peek(); int RightLessMin = col; int area = (RightLessMin - leftLessMin - 1 ) * height; maxArea = Math.max(area, maxArea); } stack.push(col); } } } return maxArea; }
方法二中,用了 LeetCode-84 的两个解法,解法三中我们把栈糅合进了原算法,那么另一种可以一样的思路吗?不行!因为栈不要求所有的高度,可以边更新,边处理。而另一种,是利用两个数组, leftLessMin [ ] 和 rightLessMin [ ]。而这两个数组的更新,是需要所有高度的。
方法二中,我们更新一次 heights,就利用之前的算法,求一遍 leftLessMin [ ] 和 rightLessMin [ ],然后更新面积。而其实,我们求 leftLessMin [ ] 和 rightLessMin [ ]可以利用之前的 leftLessMin [ ] 和 rightLessMin [ ] 来更新本次的。
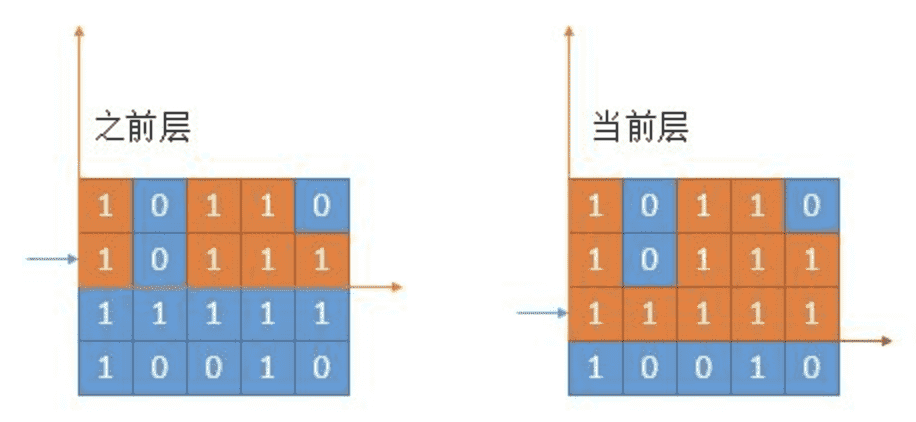
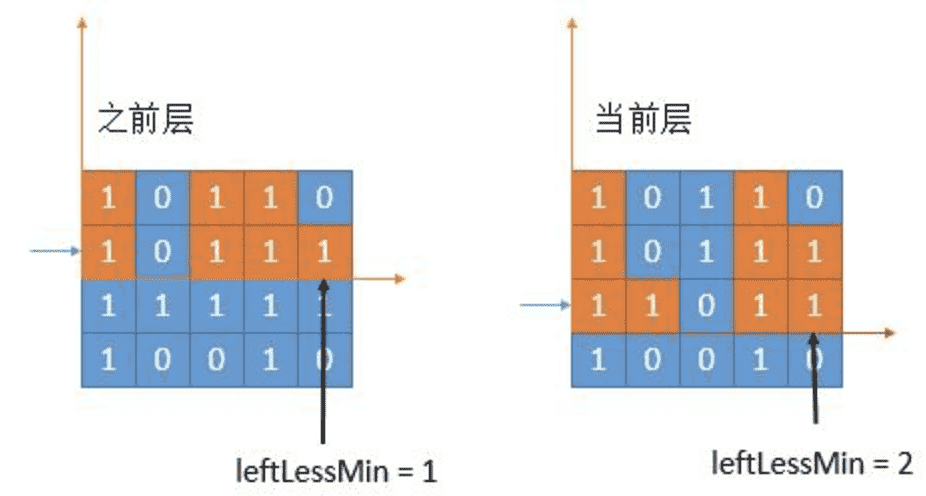
我们回想一下 leftLessMin [ ] 和 rightLessMin [ ] 的含义, leftLessMin [ i ] 代表左边第一个比当前柱子矮的下标,如下图橙色柱子时当前遍历的柱子。rightLessMin [ ]时右边第一个。
left 和 right 是对称关系,下边只考虑 left 的求法。
如下图,如果当前新增的层全部是 1,当然这是最完美的情况,那么 leftLessMin [ ] 根本不需要改变。
然而事实是残酷的,一定会有0出现。
我们考虑最后一个柱子的更新。上一层的 leftLessMin = 1,也就是蓝色 0 的位置是第一个比它低的柱子。但是在当前层,由于中间出现了 0。所以不再是之前的 leftLessMin ,而是和上次出现 0 的位置进行比较(因为 0 一定比当前柱子小),谁的下标大,更接近当前柱子,就选择谁。上图中出现 0 的位置是 2,之前的 leftLessMin 是 1,选一个较大的,那就是 2 了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 public int maximalRectangle4 (char [][] matrix) if (matrix.length == 0 ) { return 0 ; } int maxArea = 0 ; int cols = matrix[0 ].length; int [] leftLessMin = new int [cols]; int [] rightLessMin = new int [cols]; Arrays.fill(leftLessMin, -1 ); Arrays.fill(rightLessMin, cols); int [] heights = new int [cols]; for (int row = 0 ; row < matrix.length; row++) { for (int col = 0 ; col < cols; col++) { if (matrix[row][col] == '1' ) { heights[col] += 1 ; } else { heights[col] = 0 ; } } int boundary = -1 ; for (int col = 0 ; col < cols; col++) { if (matrix[row][col] == '1' ) { leftLessMin[col] = Math.max(leftLessMin[col], boundary); } else { leftLessMin[col] = -1 ; boundary = col; } } boundary = cols; for (int col = cols - 1 ; col >= 0 ; col--) { if (matrix[row][col] == '1' ) { rightLessMin[col] = Math.min(rightLessMin[col], boundary); } else { rightLessMin[col] = cols; boundary = col; } } for (int col = cols - 1 ; col >= 0 ; col--) { int area = (rightLessMin[col] - leftLessMin[col] - 1 ) * heights[col]; maxArea = Math.max(area, maxArea); } } return maxArea; }
🔗 给定三个字符串 s1, s2, s3, 验证 s3 是否是由 s1 和 s2 交错组成的。
示例 1:
输入: s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbcbcac”
示例 2:
输入: s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbbaccc”
设状态 d p [ i ] [ j ] dp[i][j] d p [ i ] [ j ] s 1 [ 0 , i ] s1[0,i] s 1 [ 0 , i ] s 2 [ 0 , j ] s2[0,j] s 2 [ 0 , j ] s 3 [ 0 , i + j ] s3[0,i+j] s 3 [ 0 , i + j ]
如果 s 1 s1 s 1 s 3 s3 s 3 d p [ i ] [ j ] = d p [ i − 1 ] [ j ] dp[i][j] = dp[i-1][j] d p [ i ] [ j ] = d p [ i − 1 ] [ j ]
如果 s 2 s2 s 2 s 3 s3 s 3 d p [ i ] [ j ] = d p [ i ] [ j − 1 ] dp[i][j] = dp[i][j-1] d p [ i ] [ j ] = d p [ i ] [ j − 1 ]
因此状态转移方程如下:
d p [ i ] [ j ] = ( s 1 [ i − 1 ] = = s 3 [ i + j − 1 ] & & d p [ i − 1 ] [ j ] ) ∣ ∣ ( s 2 [ j − 1 ] = = s 3 [ i + j − 1 ] & & d p [ i ] [ j − 1 ] ) dp[i][j] = (s1[i-1]==s3[i+j-1] \ \&\& \ dp[i-1][j]) \ || \ (s2[j-1]==s3[i+j-1] \ \&\& \ dp[i][j-1]) d p [ i ] [ j ] = ( s 1 [ i − 1 ] = = s 3 [ i + j − 1 ] & & d p [ i − 1 ] [ j ] ) ∣ ∣ ( s 2 [ j − 1 ] = = s 3 [ i + j − 1 ] & & d p [ i ] [ j − 1 ] )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution public boolean isInterleave (String s1, String s2, String s3) if (s1.length() + s2.length() != s3.length()){ return false ; } boolean [][] dp = new boolean [s1.length() + 1 ][s2.length() + 1 ]; dp[0 ][0 ] = true ; for (int i = 1 ; i <= s1.length(); ++i){ dp[i][0 ] = s3.charAt(i - 1 ) == s1.charAt(i - 1 ) && dp[i - 1 ][0 ]; } for (int i = 1 ; i <= s2.length(); ++i){ dp[0 ][i] = s3.charAt(i - 1 ) == s2.charAt(i - 1 ) && dp[0 ][i - 1 ]; } for (int i = 1 ; i <= s1.length(); ++i){ for (int j = 1 ; j <= s2.length(); ++j){ if (dp[i][j-1 ] && s3.charAt(i+j-1 ) == s2.charAt(j-1 )){ dp[i][j] = true ; continue ; } if (dp[i-1 ][j] && s3.charAt(i+j-1 ) == s1.charAt(i-1 )){ dp[i][j] = true ; continue ; } dp[i][j] = false ; } } return dp[s1.length()][s2.length()]; } }
🔗 给定一个字符串 s1,我们可以把它递归地分割成两个非空子字符串,从而将其表示为二叉树。
下图是字符串 s1 = “great” 的一种可能的表示形式。
1 2 3 4 5 6 7 great / \ gr eat / \ / \ g r e at / \ a t
在扰乱这个字符串的过程中,我们可以挑选任何一个非叶节点,然后交换它的两个子节点。
例如,如果我们挑选非叶节点 “gr” ,交换它的两个子节点,将会产生扰乱字符串 “rgeat” 。
1 2 3 4 5 6 7 rgeat / \ rg eat / \ / \ r g e at / \ a t
我们将 "rgeat” 称作 “great” 的一个扰乱字符串。
同样地,如果我们继续交换节点 “eat” 和 “at” 的子节点,将会产生另一个新的扰乱字符串 “rgtae” 。
1 2 3 4 5 6 7 rgtae / \ rg tae / \ / \ r g ta e / \ t a
我们将 "rgtae” 称作 “great” 的一个扰乱字符串。
给出两个长度相等的字符串 s1 和 s2,判断 s2 是否是 s1 的扰乱字符串。
示例 1:
输入: s1 = “great”, s2 = “rgeat”
示例 2:
输入: s1 = “abcde”, s2 = “caebd”
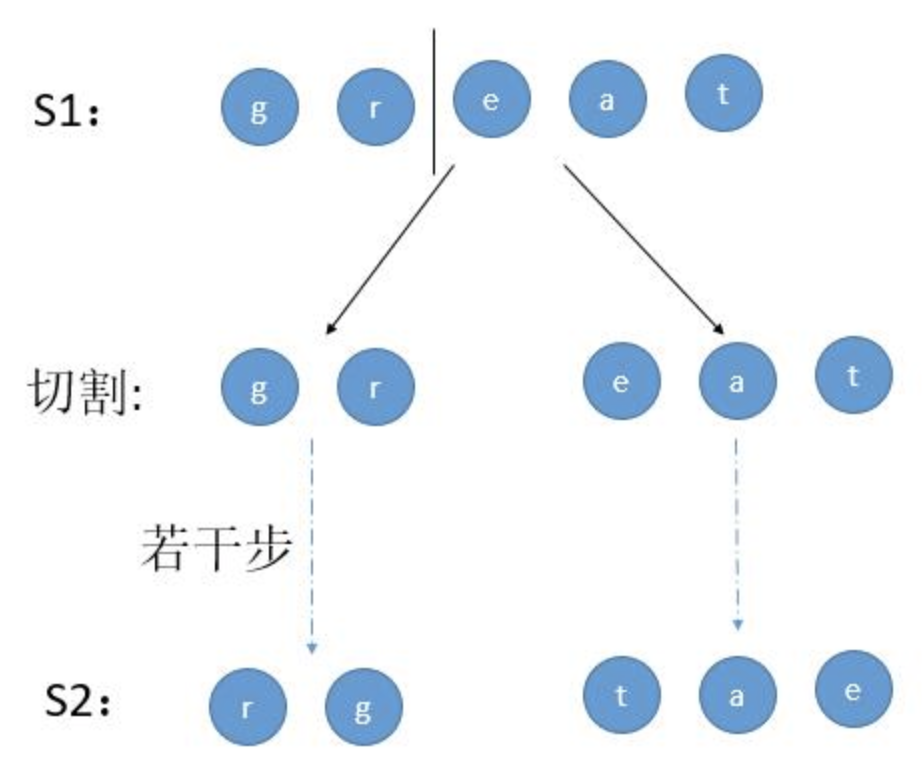
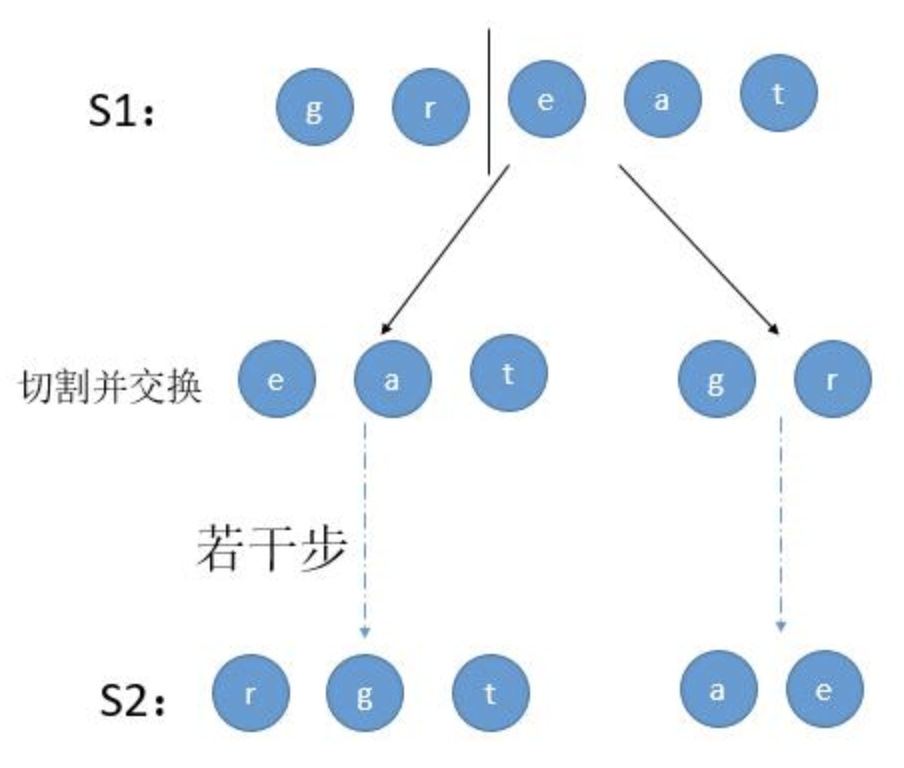
这道题利用递归的思想去解,假如两个字符串 great 和 rgeat。考虑其中的一种切割方式。
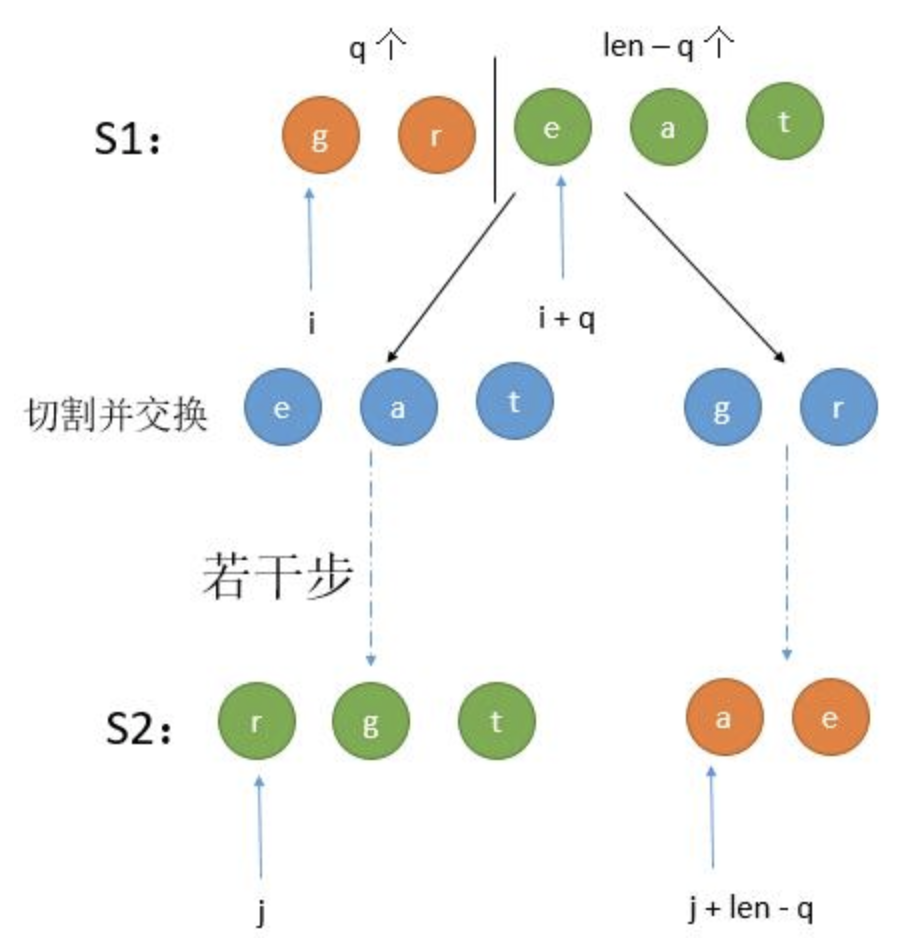
第 1 种情况:S1 切割为两部分,然后进行若干步切割交换,最后判断两个子树分别是否能变成 S2 的两部分。
第 2 种情况:S1 切割并且交换为两部分,然后进行若干步切割交换,最后判断两个子树是否能变成 S2 的两部分。
我们只需要遍历所有的切割点即可。基于此,我们可以用 memoization 技术,把递归过程中的结果存储起来,如果第二次递归过来,直接返回结果即可,无需重复递归。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 public boolean isScramble (String s1, String s2) HashMap<String, Integer> memoization = new HashMap<>(); return isScrambleRecursion(s1, s2, memoization); } public boolean isScrambleRecursion (String s1, String s2, HashMap<String, Integer> memoization) int ret = memoization.getOrDefault(s1 + "#" + s2, -1 ); if (ret == 1 ) { return true ; } else if (ret == 0 ) { return false ; } if (s1.length() != s2.length()) { memoization.put(s1 + "#" + s2, 0 ); return false ; } if (s1.equals(s2)) { memoization.put(s1 + "#" + s2, 1 ); return true ; } int [] letters = new int [26 ]; for (int i = 0 ; i < s1.length(); i++) { letters[s1.charAt(i) - 'a' ]++; letters[s2.charAt(i) - 'a' ]--; } for (int i = 0 ; i < 26 ; i++){ if (letters[i] != 0 ) { memoization.put(s1 + "#" + s2, 0 ); return false ; } } for (int i = 1 ; i < s1.length(); i++) { if (isScramble(s1.substring(0 , i), s2.substring(0 , i)) && isScramble(s1.substring(i), s2.substring(i))) { memoization.put(s1 + "#" + s2, 1 ); return true ; } if (isScramble(s1.substring(0 , i), s2.substring(s2.length() - i)) && isScramble(s1.substring(i), s2.substring(0 , s2.length() - i))) { memoization.put(s1 + "#" + s2, 1 ); return true ; } } memoization.put(s1 + "#" + s2, 0 ); return false ; }
既然是递归(压栈压栈压栈-出栈出栈出栈),我们可以利用动态规划的思想,省略压栈的过程,直接从底部往上走。
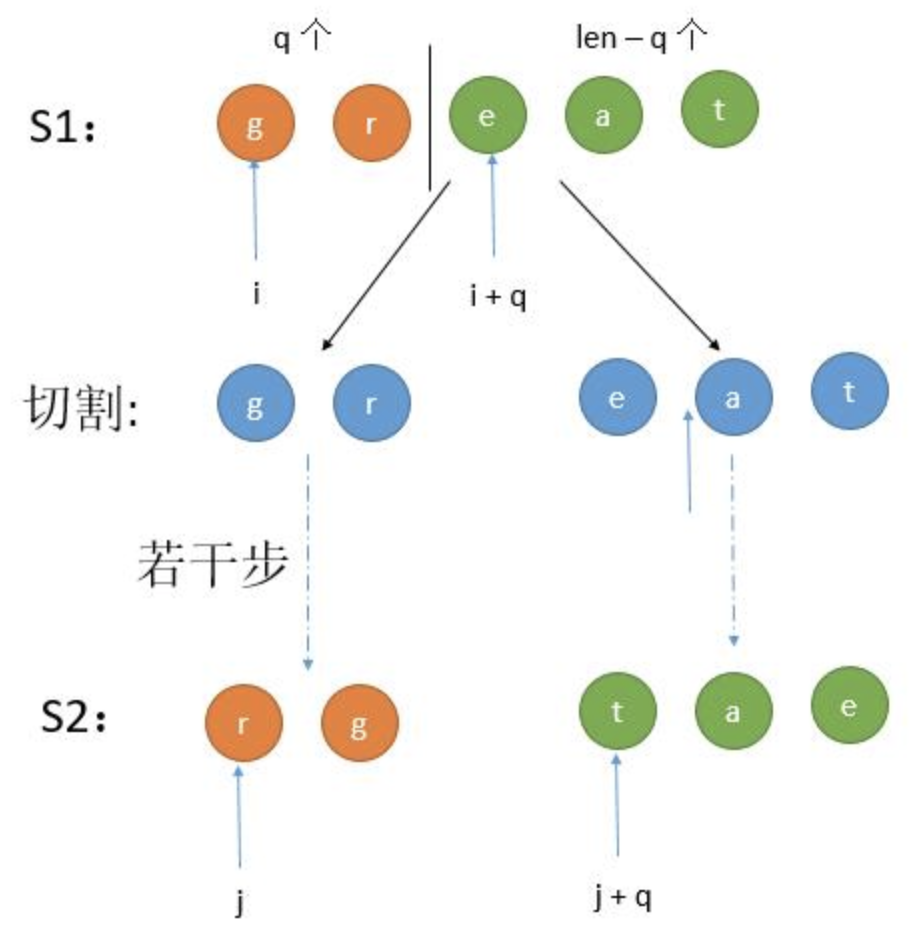
我们用 d p [ l e n ] [ i ] [ j ] dp[len][i][j] d p [ l e n ] [ i ] [ j ] s 1 [ i , i + l e n ] s1[i,i+len] s 1 [ i , i + l e n ] s 2 [ j , j + l e n ] s2[j,j+len] s 2 [ j , j + l e n ] s 1 s1 s 1 s 2 s2 s 2
假设左半部分长度是 q,那么 d p [ l e n ] [ i ] [ j ] = d p [ q ] [ i ] [ j ] & & d p [ l e n − q ] [ i + q ] [ j + q ] dp[len][i][j]=dp[q][i][j] \ \&\& \ dp[len-q][i+q][j+q] d p [ l e n ] [ i ] [ j ] = d p [ q ] [ i ] [ j ] & & d p [ l e n − q ] [ i + q ] [ j + q ] s 1 s1 s 1 s 2 s2 s 2 s 1 s1 s 1 s 2 s2 s 2
假设左半部分长度是 q,那么 d p [ l e n ] [ i ] [ j ] = d p [ q ] [ i ] [ j + l e n − q ] & & d p [ l e n − q ] [ i + q ] [ j ] dp[len][i][j] = dp[q][i][j+len-q] \ \&\& \ dp[len-q][i+q][j] d p [ l e n ] [ i ] [ j ] = d p [ q ] [ i ] [ j + l e n − q ] & & d p [ l e n − q ] [ i + q ] [ j ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 public boolean isScramble4 (String s1, String s2) if (s1.length() != s2.length()) { return false ; } if (s1.equals(s2)) { return true ; } int [] letters = new int [26 ]; for (int i = 0 ; i < s1.length(); i++) { letters[s1.charAt(i) - 'a' ]++; letters[s2.charAt(i) - 'a' ]--; } for (int i = 0 ; i < 26 ; i++) { if (letters[i] != 0 ) { return false ; } } int length = s1.length(); boolean [][][] dp = new boolean [length + 1 ][length][length]; for (int len = 1 ; len <= length; len++) { for (int i = 0 ; i + len <= length; i++) { for (int j = 0 ; j + len <= length; j++) { if (len == 1 ) { dp[len][i][j] = s1.charAt(i) == s2.charAt(j); } else { for (int q = 1 ; q < len; q++) { dp[len][i][j] = dp[q][i][j] && dp[len - q][i + q][j + q] || dp[q][i][j + len - q] && dp[len - q][i + q][j]; if (dp[len][i][j]) { break ; } } } } } } return dp[length][0 ][0 ]; }
🔗 给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例:
1 2 3 4 5 6 7 8 输入: [ [1,3,1], [1,5,1], [4,2,1] ] 输出: 7 解释: 因为路径 1→3→1→1→1 的总和最小。
传统的二维的DP问题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution public int minPathSum (int [][] grid) for (int i = 1 ; i < grid.length; ++i){ grid[i][0 ] += grid[i-1 ][0 ]; } for (int i = 1 ; i < grid[0 ].length; ++i){ grid[0 ][i] += grid[0 ][i-1 ]; } for (int row = 1 ; row < grid.length; ++row){ for (int col = 1 ; col < grid[0 ].length; ++col){ grid[row][col] += Math.min(grid[row-1 ][col], grid[row][col-1 ]); } } return grid[grid.length-1 ][grid[0 ].length-1 ]; } }
🔗 给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
示例 1:
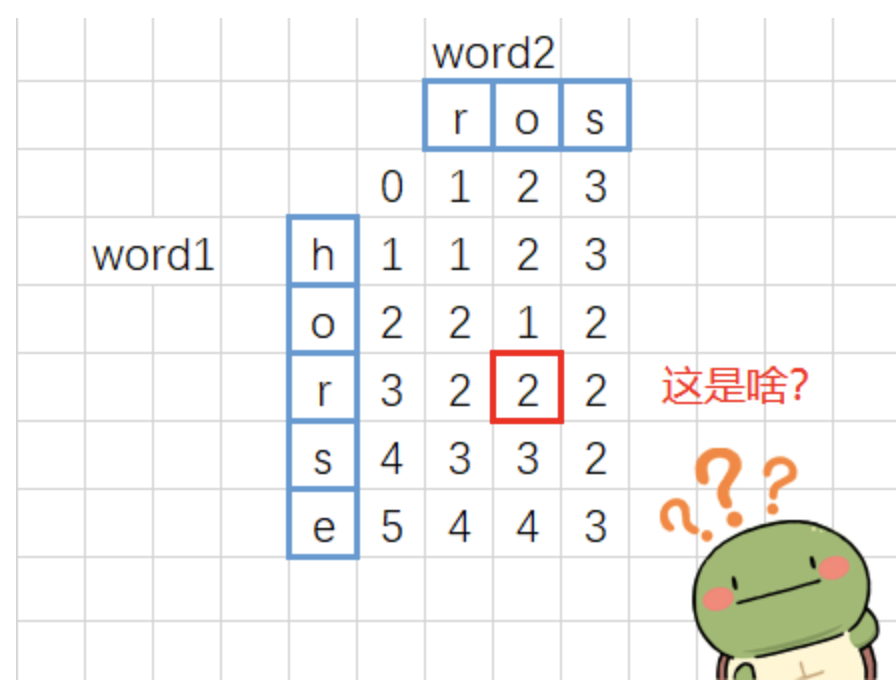
1 2 3 4 5 6 输入:word1 = "horse" , word2 = "ros" 输出:3 解释: horse -> rorse (将 'h' 替换为 'r' ) rorse -> rose (删除 'r' ) rose -> ros (删除 'e' )
示例 2:
1 2 3 4 5 6 7 8 输入:word1 = "intention" , word2 = "execution" 输出:5 解释: intention -> inention (删除 't' ) inention -> enention (将 'i' 替换为 'e' ) enention -> exention (将 'n' 替换为 'x' ) exention -> exection (将 'n' 替换为 'c' ) exection -> execution (插入 'u' )
我们可以对任意一个单词进行三种操作:
题目给定了两个单词,设为 A 和 B,这样我们就能够六种操作方法。
但我们可以发现,如果我们有单词 A 和单词 B:
对单词 A 删除一个字符和对单词 B 插入一个字符是等价的。例如当单词 A 为 doge,单词 B 为 dog 时,我们既可以删除单词 A 的最后一个字符 e,得到相同的 dog,也可以在单词 B 末尾添加一个字符 e,得到相同的 doge;
同理,对单词 B 删除一个字符和对单词 A 插入一个字符也是等价的;对单词 A 替换一个字符和对单词 B 替换一个字符是等价的。例如当单词 A 为 bat,单词 B 为 cat 时,我们修改单词 A 的第一个字母 b -> c,和修改单词 B 的第一个字母 c -> b 是等价的。
这样以来,本质不同的操作实际上只有三种 :
在单词 A 中插入一个字符;
在单词 B 中插入一个字符;
修改单词 A 的一个字符。
这样以来,我们就可以把原问题转化为规模较小的子问题。我们用 A = horse,B = ros 作为例子,来看一看是如何把这个问题转化为规模较小的若干子问题的。
在单词 A 中插入一个字符:如果我们知道 horse 到 ro 的编辑距离为 a,那么显然 horse 到 ros 的编辑距离不会超过 a + 1。这是因为我们可以在 a 次操作后将 horse 和 ro 变为相同的字符串,只需要额外的 1 次操作,在单词 A 的末尾添加字符 s,就能在 a + 1 次操作后将 horse 和 ros 变为相同的字符串;
在单词 B 中插入一个字符:如果我们知道 hors 到 ros 的编辑距离为 b,那么显然 horse 到 ros 的编辑距离不会超过 b + 1,原因同上;
修改单词 A 的一个字符:如果我们知道 hors 到 ro 的编辑距离为 c,那么显然 horse 到 ros 的编辑距离不会超过 c + 1,原因同上。
那么从 horse 变成 ros 的编辑距离应该为 m i n ( a + 1 , b + 1 , c + 1 ) min(a + 1, b + 1, c + 1) m i n ( a + 1 , b + 1 , c + 1 )
**注意:**为什么我们总是在单词 A 和 B 的末尾插入或者修改字符,能不能在其它的地方进行操作呢?答案是可以的,但是我们知道,操作的顺序是不影响最终的结果的。例如对于单词 cat,我们希望在 c 和 a 之间添加字符 d 并且将字符 t 修改为字符 b,那么这两个操作无论为什么顺序,都会得到最终的结果 cdab。
你可能觉得 horse 到 ro 这个问题也很难解决。但是没关系,我们可以继续用上面的方法拆分这个问题,对于这个问题拆分出来的所有子问题,我们也可以继续拆分,直到:
因此,我们就可以使用动态规划 来解决这个问题了。我们用 d p [ i ] [ j ] dp[i][j] d p [ i ] [ j ]
如上所述,当我们获得 d p [ i ] [ j − 1 ] dp[i][j-1] d p [ i ] [ j − 1 ] d p [ i − 1 ] [ j ] dp[i-1][j] d p [ i − 1 ] [ j ] d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] d p [ i − 1 ] [ j − 1 ] d p [ i ] [ j ] dp[i][j] d p [ i ] [ j ]
若 A [ i ] = B [ j ] A[i] = B[j] A [ i ] = B [ j ] d p [ i ] [ j ] = d p [ i − 1 ] [ j − 1 ] dp[i][j] = dp[i-1][j-1] d p [ i ] [ j ] = d p [ i − 1 ] [ j − 1 ]
若 A [ i ] ≠ B [ j ] A[i] \neq B[j] A [ i ] = B [ j ] d p [ i ] [ j ] = m i n { d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] , d p [ i − 1 ] [ j − 1 ] } + 1 dp[i][j] = min\{dp[i-1][j], dp[i][j-1], dp[i-1][j-1]\} + 1 d p [ i ] [ j ] = m i n { d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] , d p [ i − 1 ] [ j − 1 ] } + 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution public int minDistance (String word1, String word2) int [][] dp = new int [word1.length()+1 ][word2.length()+1 ]; for (int i = 0 ; i < dp.length; ++i){ dp[i][0 ] = i; } for (int j = 0 ; j < dp[0 ].length; ++j){ dp[0 ][j] = j; } for (int i = 1 ; i < dp.length; ++i){ for (int j = 1 ; j < dp[0 ].length; ++j){ if (word1.charAt(i-1 ) == word2.charAt(j-1 )){ dp[i][j] = dp[i-1 ][j-1 ]; }else { dp[i][j] = Math.min(dp[i-1 ][j-1 ], Math.min(dp[i-1 ][j], dp[i][j-1 ])) + 1 ; } } } return dp[dp.length-1 ][dp[0 ].length-1 ]; } }
🔗 一条包含字母 A-Z 的消息通过以下方式进行了编码:
1 2 3 4 'A' -> 1'B' -> 2... 'Z' -> 26
给定一个只包含数字的非空字符串,请计算解码方法的总数。
示例 1:
1 2 3 输入: "12" 输出: 2 解释: 它可以解码为 "AB" (1 2)或者 "L" (12)。
示例 2:
1 2 3 输入: "226" 输出: 3 解释: 它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。
本题为反方向考虑的动态规划问题!!!
i f n u m [ i ] = 0 , d p [ i ] = 0 if \ num[i] = 0, dp[i]=0 i f n u m [ i ] = 0 , d p [ i ] = 0
i f n u m [ i ] + n u m [ i + 1 ] ≤ 26 , d p [ i ] = d p [ i + 1 ] + d p [ i + 2 ] ; if \ num[i] + num[i+1] \leq 26 , dp[i]=dp[i+1]+dp[i+2]; i f n u m [ i ] + n u m [ i + 1 ] ≤ 2 6 , d p [ i ] = d p [ i + 1 ] + d p [ i + 2 ] ;
e l s e d p [ i ] = d p [ i + 1 ] else \ dp[i]=dp[i+1] e l s e d p [ i ] = d p [ i + 1 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution public int numDecodings (String s) int [] dp = new int [s.length()+1 ]; dp[s.length()] = 1 ; for (int i = s.length()-1 ; i >= 0 ; --i){ if (s.charAt(i) == '0' ){ dp[i] = 0 ; }else { if (i == s.length() - 1 ){ dp[i] = 1 ; continue ; } int two = (s.charAt(i) - '0' ) * 10 + (s.charAt(i + 1 ) - '0' ); if (two <= 26 ){ dp[i] = dp[i+1 ] + dp[i+2 ]; }else { dp[i] = dp[i+1 ]; } } } return dp[0 ]; } }
🔗 给定一个字符串 S 和一个字符串 T,计算在 S 的子序列中 T 出现的个数。
一个字符串的一个子序列是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。(例如,“ACE” 是 “ABCDE” 的一个子序列,而 “AEC” 不是)
题目数据保证答案符合 32 位带符号整数范围。
示例 1:
1 2 3 4 5 6 7 8 9 10 11 输入:S = "rabbbit" , T = "rabbit" 输出:3 解释: 如下图所示, 有 3 种可以从 S 中得到 "rabbit" 的方案。 (上箭头符号 ^ 表示选取的字母) rabbbit ^^^^ ^^ rabbbit ^^ ^^^^ rabbbit ^^^ ^^^
示例 2:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 输入:S = "babgbag" , T = "bag" 输出:5 解释: 如下图所示, 有 5 种可以从 S 中得到 "bag" 的方案。 (上箭头符号 ^ 表示选取的字母) babgbag ^^ ^ babgbag ^^ ^ babgbag ^ ^^ babgbag ^ ^^ babgbag ^^^
设状态为 d p [ i ] [ j ] dp[i][j] d p [ i ] [ j ] T [ 0 , j ] T[0,j] T [ 0 , j ] S [ 0 , i ] S[0,i] S [ 0 , i ]
则状态转移方程 为:
首先无论 S [ i ] S[i] S [ i ] T [ j ] T[j] T [ j ]
若 S [ i ] ≠ T [ j ] S[i] \neq T[j] S [ i ] = T [ j ] d p [ i ] [ j ] = d p [ i − 1 ] [ j ] dp[i][j] = dp[i-1][j] d p [ i ] [ j ] = d p [ i − 1 ] [ j ]
若 S [ i ] = T [ j ] S[i]=T[j] S [ i ] = T [ j ] d p [ i ] [ j ] = d p [ i − 1 ] [ j ] + d p [ i − 1 ] [ j − 1 ] dp[i][j]=dp[i-1][j]+dp[i-1][j-1] d p [ i ] [ j ] = d p [ i − 1 ] [ j ] + d p [ i − 1 ] [ j − 1 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class Solution public int numDistinct (String s, String t) int [][] dp = new int [t.length() + 1 ][s.length() + 1 ]; for (int j = 0 ; j < s.length() + 1 ; j++) { dp[0 ][j] = 1 ; } for (int i = 1 ; i < t.length() + 1 ; i++) { for (int j = 1 ; j < s.length() + 1 ; j++) { if (t.charAt(i - 1 ) == s.charAt(j - 1 )) { dp[i][j] = dp[i - 1 ][j - 1 ] + dp[i][j - 1 ]; } else { dp[i][j] = dp[i][j - 1 ]; } } } return dp[t.length()][s.length()]; } public int numDistinct2 (String s, String t) int [] dp = new int [t.length()+1 ]; dp[0 ] = 1 ; for (int i = 0 ; i < s.length(); ++i){ for (int j = t.length() - 1 ; j >= 0 ; --j){ dp[j+1 ] += s.charAt(i) == t.charAt(j) ? dp[j] : 0 ; } } return dp[t.length()]; } }
🔗 给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
说明:
拆分时可以重复使用字典中的单词。
示例 1:
1 2 3 输入: s = "leetcode" , wordDict = ["leet" , "code" ] 输出: true 解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code" 。
示例 2:
1 2 3 4 输入: s = "applepenapple" , wordDict = ["apple" , "pen" ] 输出: true 解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple" 。 注意你可以重复使用字典中的单词。
示例 3:
1 2 输入: s = "catsandog" , wordDict = ["cats" , "dog" , "sand" , "and" , "cat" ] 输出: false
设状态 d p [ i ] dp[i] d p [ i ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution public boolean wordBreak (String s, List<String> wordDict) boolean [] dp = new boolean [s.length() + 1 ]; dp[0 ] = true ; for (int i = 1 ; i <= s.length(); i++) { for (int j = 0 ; j < i; j++) { if (dp[j] && wordDict.contains(s.substring(j, i))) { dp[i] = true ; break ; } } } return dp[s.length()]; } }
🔗 给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict,在字符串中增加空格来构建一个句子,使得句子中所有的单词都在词典中。返回所有这些可能的句子。
说明:
分隔时可以重复使用字典中的单词。
示例 1:
1 2 3 4 5 6 7 8 输入: s = "catsanddog" wordDict = ["cat" , "cats" , "and" , "sand" , "dog" ] 输出: [ "cats and dog" , "cat sand dog" ]
示例 2:
1 2 3 4 5 6 7 8 9 10 输入: s = "pineapplepenapple" wordDict = ["apple" , "pen" , "applepen" , "pine" , "pineapple" ] 输出: [ "pine apple pen apple" , "pineapple pen apple" , "pine applepen apple" ] 解释: 注意你可以重复使用字典中的单词。
示例 3:
1 2 3 4 5 输入: s = "catsandog" wordDict = ["cats" , "dog" , "sand" , "and" , "cat" ] 输出: []
基于上一题进行修改,只不过状态数组 d p [ ] dp[] d p [ ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution public List<String> wordBreak (String s, List<String> wordDict) LinkedList<String>[] dp = new LinkedList[s.length() + 1 ]; LinkedList<String> initial = new LinkedList<>(); initial.add("" ); dp[0 ] = initial; for (int i = 1 ; i <= s.length(); i++) { LinkedList<String> list = new LinkedList<>(); for (int j = 0 ; j < i; j++) { if (dp[j].size() > 0 && wordDict.contains(s.substring(j, i))) { for (String l : dp[j]) { list.add(l + (l.equals("" ) ? "" : " " ) + s.substring(j, i)); } } } dp[i] = list; } return dp[s.length()]; } }